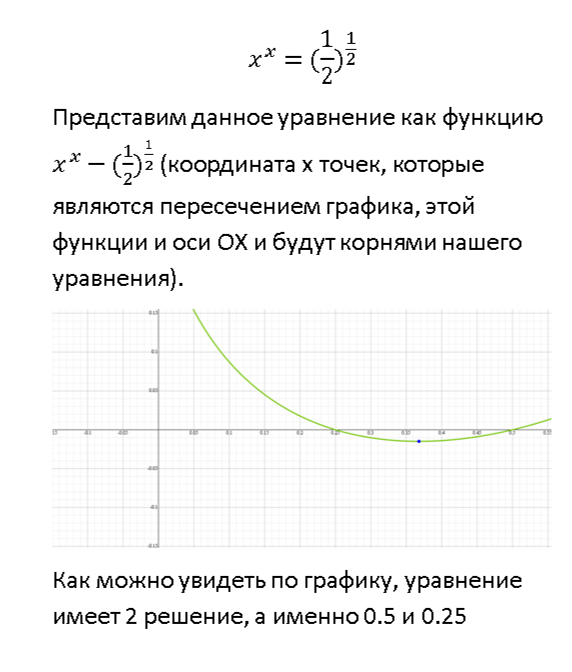
абстрактный вопрос, разрешимость в радикалах, теорема Абеля о неразрешимости уравнений в радикалах и
Hiop
26/12/25 Птн 10:32:41
№
1
"Элемент a поля F называется выразимым в радикалах над подполем G поля, если существует алгебраическое выражение, в которое в качестве чисел входят только элементы поля G, значение которого равно a. В случае, если в поле F корень является многозначной функцией, считается достаточным равенство числа a хотя бы одному из возможных значений алгебраического выражения." (источник:https://ru.wikipedia.org/wiki/).
Если простыми словами, то термин "выразимость в радикалах" означает возможность уравнения привести к виду x=t (где t - это какое либо выражение не содержащее x).
Например уравнение 5 степени и выше не выразимы в радикалах ( по теореме Абеля или Абеля-Руффини).
Я уже 2 года маюсь над одним вопрос, а именно: "имеет ли уравнение xx=0.50.5 общее алгебраическое решение (или же выражаясь более строго: выразимо ли это уравнение в радикалах)?"
Я понимаю интуитивно, что оно его не имеет этого алгебраического решения, но в силу своих знаний не могу доказать это строго (используя группы Галуа и так далее).
Его корнями являются числа 1/2 и 1/4, только как к ним придти алгебраически?
нА картинке, которую я прикрепил есть графическое решение данного уравнения.
Ну и ерунду ты написал. Конечно твои корни выразимы в радикалах. Потому что x1 =1/2, x2 = 1/4. Справа от знака равенства те самые алгебраические выражения, в которые входят только элементы поля G, т.е. рациональных чисел. Значит корни твоего уравнения - алгебраические числа, и оно разрешимо в радикалах.
Дебильный термин. Потому что по этом определению в радикалах все что угодно будет разрешимо в полях R/C. А про что А-Р утверждает это другая разрешимость - там требуется существование формулы для уравнения в общем случае. ХЗ есть ли где строгое определение этого понятия. Там дальше они в википедии вроде бы пытаются его дать, но кмк говна они там намесили какого-то (статья попахивает ориджинал ресерчем).
Окей хорошо, раз это уравнение выразимо в радикалах, то как из исходного уравнения, ты выйдешь к x=1/2 или x=1/4?
Если x^x = (1/2)^(1/2), то x = 1/2 это решение уравнения. С другой стороны, мы имеем x^x = (1/2)^(1/2) = ((1/2)^2)^(1/4) = (1/4)^(1/4), т.е. x = 1/4 это еще одно решение. Без анализа показать, что это все решения, наверное, нельзя.
Если тебя интересует, является ли функция x^x алгебраической, то достаточно показать, что функция e^x не является алгебраической. Потом ты можешь показать, что обратная функция к x^x не может быть алгебраической, т.е. не существует "формулы", решающей "x^x=a", в которой нет ничего кроме арифметических операций и корней.
мимо